Collatz conjecture sequence length distribution
Jun 15, 2022
자연수 n에 대해 f(n) = 3n + 1 (n이 홀수), n/2 (n이 짝수)를 정의하자. 이 때 어떠한 자연수 n을 가져오더라도 f(…)을 계속 적용하다보면 1 (->4->2->1->…) 로 끝난다는 추측이다. 컴퓨터로 돌려봤을 때는 2^68 까지는 반례가 없다고 한다. (wiki)
파이썬에서 함수 op_collatz(n)을 정의하고,
def op_collatz(n):
ret = []
while n >= 1:
ret.append(n)
if n == 1:
break
if n % 2 == 0:
n = n // 2
else:
n = 3 * n + 1
return ret
1 ~ 29까지의 수열 (n, f(n), f(f(n)), …)을 돌려보면,
for i in range(1, 30):
a = op_collatz(i)
print(i, len(a), "→".join(map(str, a)), sep="\t")
아래와 같은 결과를 얻는다.
1 1 1
2 2 2→1
3 8 3→10→5→16→8→4→2→1
4 3 4→2→1
5 6 5→16→8→4→2→1
6 9 6→3→10→5→16→8→4→2→1
7 17 7→22→11→34→17→52→26→13→40→20→10→5→16→8→4→2→1
8 4 8→4→2→1
9 20 9→28→14→7→22→11→34→17→52→26→13→40→20→10→5→16→8→4→2→1
10 7 10→5→16→8→4→2→1
11 15 11→34→17→52→26→13→40→20→10→5→16→8→4→2→1
12 10 12→6→3→10→5→16→8→4→2→1
13 10 13→40→20→10→5→16→8→4→2→1
14 18 14→7→22→11→34→17→52→26→13→40→20→10→5→16→8→4→2→1
15 18 15→46→23→70→35→106→53→160→80→40→20→10→5→16→8→4→2→1
16 5 16→8→4→2→1
17 13 17→52→26→13→40→20→10→5→16→8→4→2→1
18 21 18→9→28→14→7→22→11→34→17→52→26→13→40→20→10→5→16→8→4→2→1
19 21 19→58→29→88→44→22→11→34→17→52→26→13→40→20→10→5→16→8→4→2→1
20 8 20→10→5→16→8→4→2→1
21 8 21→64→32→16→8→4→2→1
22 16 22→11→34→17→52→26→13→40→20→10→5→16→8→4→2→1
23 16 23→70→35→106→53→160→80→40→20→10→5→16→8→4→2→1
24 11 24→12→6→3→10→5→16→8→4→2→1
25 24 25→76→38→19→58→29→88→44→22→11→34→17→52→26→13→40→20→10→5→16→8→4→2→1
26 11 26→13→40→20→10→5→16→8→4→2→1
27 112 27→82→41→124→62→31→94→47→142→71→214→107→322→161→484→242→121→364→182→91→274→137→412→206→103→310→155→466→233→700→350→175→526→263→790→395→1186→593→1780→890→445→1336→668→334→167→502→251→754→377→1132→566→283→850→425→1276→638→319→958→479→1438→719→2158→1079→3238→1619→4858→2429→7288→3644→1822→911→2734→1367→4102→2051→6154→3077→9232→4616→2308→1154→577→1732→866→433→1300→650→325→976→488→244→122→61→184→92→46→23→70→35→106→53→160→80→40→20→10→5→16→8→4→2→1
28 19 28→14→7→22→11→34→17→52→26→13→40→20→10→5→16→8→4→2→1
29 19 29→88→44→22→11→34→17→52→26→13→40→20→10→5→16→8→4→2→1
우선 수학적 귀납법으로 생각해본다면 1 <= k <= n 까지 콜라츠 추측이 성립한다고 가정했을 때, n보다 작은 값을 단 한 번이라도 밟으면 (f를 계속 적용) 1로 끝난다고 할 수 있다. 예를 들어 14는 이미 7이 1로 끝나는 것을 확인해봤으니, 굳이 다시 계산하지 않아도 된다. 홀수의 경우는 상황이 다르다. 다시 말해 n = 2m + 1 (m은 음이 아닌 정수)에서 f(n) = f(2m+1) = 3*(2m+1)+1 = 6m+4 = 2*(3m+2)가 되고, f(f(n))은 3m+2가 된다. 이 값은 2m+1+m+1 이므로 원래 값보다 더 큰 값이다. 예를 들어 25의 경우 m=12이므로, f를 두 번 적용하면 3*12+2 = 38 을 얻게 된다. 운이 좋아 3m+2가 여러 번 2로 나누어 떨어져서 2m+1 보다 작게 되면 collapse된다고 볼 수 있다. 그런데 27의 경우는 27 -> … -> 41 -> … -> 31 -> … -> 47 -> … -> 71 -> … -> 107 -> … 등으로 심지어 3077 -> 9232까지 지나갔다가 한참이 지나 겨우 23을 한 번 밟고 1로 끝나게 된다. 그래서 규칙을 적용시키다보면 2^q (q가 클수록 좋다)을 약수로 가지는가에 대한 문제로 볼 수 있지 않나 싶기도 하다.
증명이야 난제니까 손대면 안되겠지만 (반례가 있는지도 확실하지 않음), 수열 op_collatz(n) 이 주어졌을 때 최댓값이 원래 n에 비해 얼마나 큰지, 수열의 길이 분포는 어떤지 궁금해졌다. 원래 주어진 수에 비해 “상당히” 큰 값이 나오는 경우도 드물지만 존재한다.
op_collatz(159487) => [159487, 478462, 239231, 717694, 358847, 1076542, 538271, 1614814, 807407, 2422222, 1211111, 3633334, 1816667, 5450002, 2725001, 8175004, 4087502, 2043751, 6131254, 3065627, 9196882, 4598441, 13795324, 6897662, 3448831, 10346494, 5173247, 15519742, 7759871, 23279614, 11639807, 34919422, 17459711, 52379134, 26189567, 78568702, 39284351, 117853054, 58926527, 176779582, 88389791, 265169374, 132584687, 397754062, 198877031, 596631094, 298315547, 894946642, 447473321, 1342419964, 671209982, 335604991, 1006814974, 503407487, 1510222462, 755111231, 2265333694, 1132666847, 3398000542, 1699000271, 5097000814, 2548500407, 7645501222, 3822750611, 11468251834, 5734125917, 17202377752, 8601188876, 4300594438, 2150297219, 6450891658, 3225445829, 9676337488, 4838168744, 2419084372, 1209542186, 604771093, 1814313280, 907156640, 453578320, 226789160, 113394580, 56697290, 28348645, 85045936, 42522968, 21261484, 10630742, 5315371, 15946114, 7973057, 23919172, 11959586, 5979793, 17939380, 8969690, 4484845, 13454536, 6727268, 3363634, 1681817, 5045452, 2522726, 1261363, 3784090, 1892045, 5676136, 2838068, 1419034, 709517, 2128552, 1064276, 532138, 266069, 798208, 399104, 199552, 99776, 49888, 24944, 12472, 6236, 3118, 1559, 4678, 2339, 7018, 3509, 10528, 5264, 2632, 1316, 658, 329, 988, 494, 247, 742, 371, 1114, 557, 1672, 836, 418, 209, 628, 314, 157, 472, 236, 118, 59, 178, 89, 268, 134, 67, 202, 101, 304, 152, 76, 38, 19, 58, 29, 88, 44, 22, 11, 34, 17, 52, 26, 13, 40, 20, 10, 5, 16, 8, 4, 2, 1]
798208 = 2^9 * 1559에서 운이 좋게 2^9 를 약수로 가지고, 여기서 값이 빠르게 감소하고, op_collatz(99776) 의 결과를 재사용할 수 있게 된다.
수열의 길이에 대한 분포는 다음과 같은 모양이다. 1 <= n < 1000000에 대해 len(op_collatz(n))의 분포도를 그린 결과다.
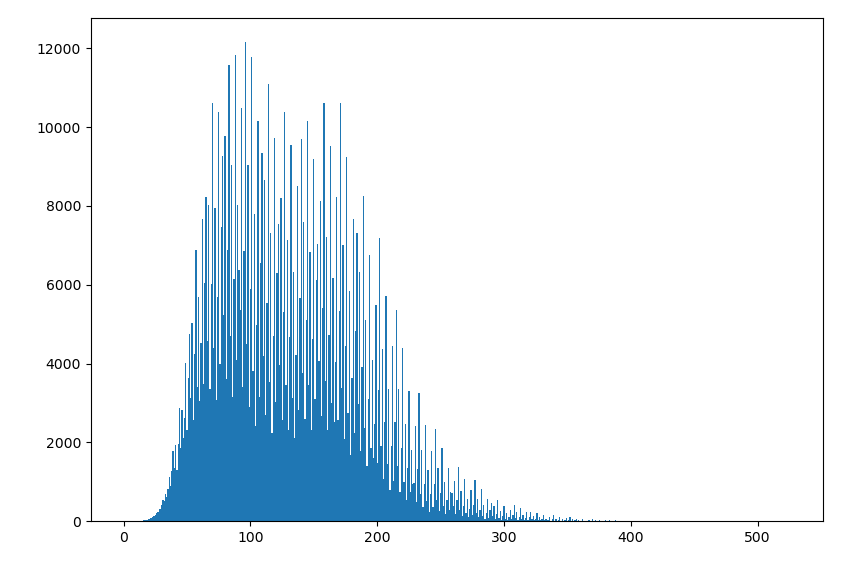
(노트) Python3 에서는 아주 큰 정수 처리도 무난하게 되는데 (unbound integer), 아주 큰 값의 인접한 정수들에 대해 len(a) 는 과연 어떨까? 이를테면 [10^n, 10^n + 10000)의 구간에 대해서 len(a)의 분포를 구해보는 것이다. n = 119 의 무지막지한 수를 넣은 결과 모두 3041의 길이를 가지는 수열이 반환되었다. 시작은 약간씩 다르지만 어느 시점에는 같은 값을 가지게 된다. 수열의 2401번 원소의 값은 676897978627712362556516626 …